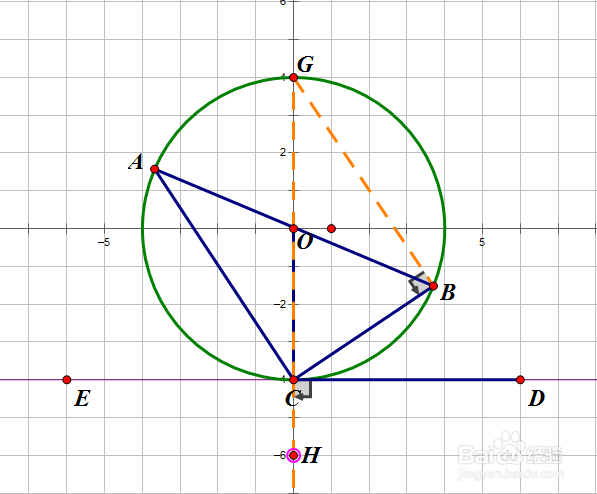
1、定理内容:顶点C在圆上一边BC与圆相交,一边CD与圆相吨易坌荐切的角叫弦切角(∠BCD)。则弦切角BCD与其夹着的弧BC所对的圆周角CAB相等。
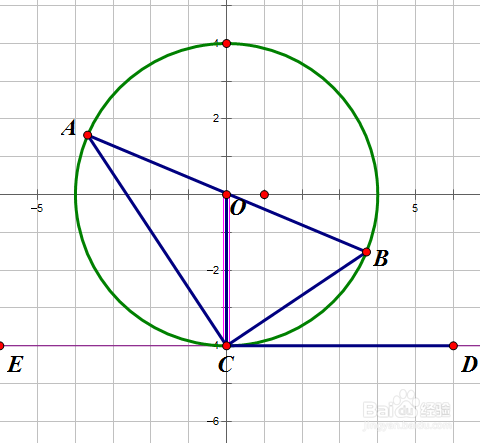
2、辅助线:做一条圆O的过点C的直径交圆于C、G,连BG
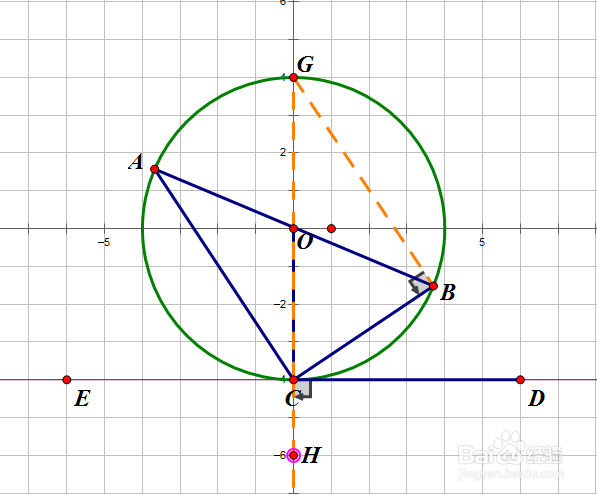
3、由于等弧对等角,所以∠BAC=∠CGB
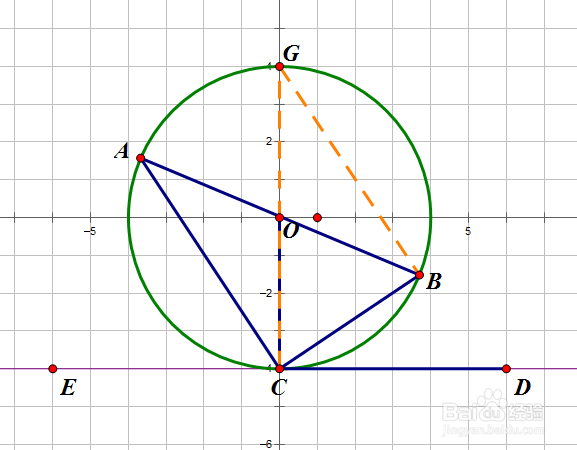
4、由于∠GBC所对的弦为直径,所以∠GBC=∠HCD=90°
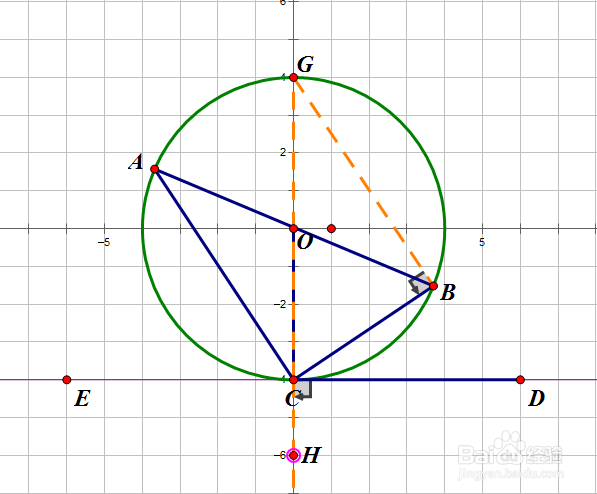
5、在△CBG中,∠CBG+∠CGB=∠BCH=∠BCD+∠HCD(外角定理)所以∠C蘅荫酸圉GB=∠BCD所以∠BCD=∠CAB得证
时间:2024-10-13 10:16:17
1、定理内容:顶点C在圆上一边BC与圆相交,一边CD与圆相吨易坌荐切的角叫弦切角(∠BCD)。则弦切角BCD与其夹着的弧BC所对的圆周角CAB相等。

2、辅助线:做一条圆O的过点C的直径交圆于C、G,连BG

3、由于等弧对等角,所以∠BAC=∠CGB

4、由于∠GBC所对的弦为直径,所以∠GBC=∠HCD=90°

5、在△CBG中,∠CBG+∠CGB=∠BCH=∠BCD+∠HCD(外角定理)所以∠C蘅荫酸圉GB=∠BCD所以∠BCD=∠CAB得证

