在概沧鲎孳卣率论和统计学中,数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小。
D(X) = E{[X - E(X)]^2}.(1)=E(X^2) - (EX)^2.(2)。
(1)式是方差的离差表示法。
(2)式表示:方差 = X^2的期望 - X的期望的平方。
相关内容:
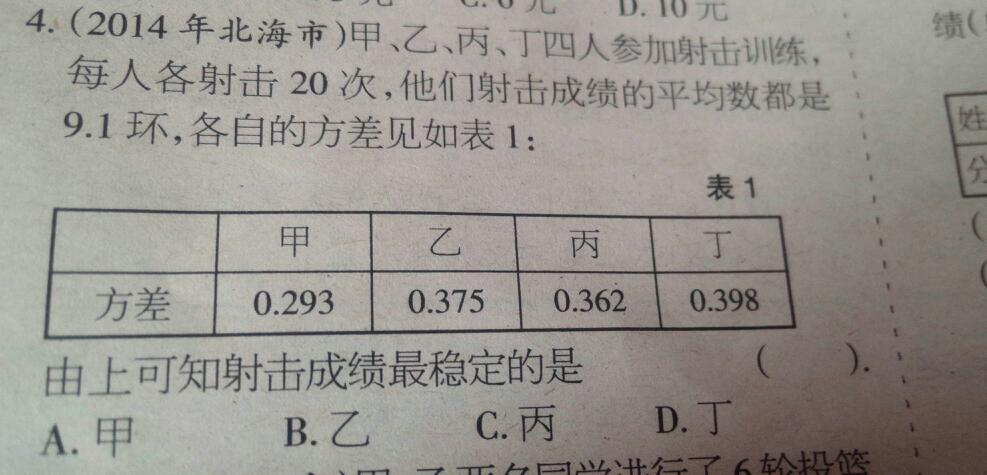
当数据分布比较分散(即数据在平均数附近波动较大)时,各个数据与平均数的差的平方和较大,方差就较大;当数据分布比较集中时,各个数据与平均数的差的平方和较小。因此方差越大,数据的波动越大;方差越小,数据的波动就越小。
用概率论的知识,不难得知,甲获胜的可能性大,乙获胜的可能性小。
因为甲输掉后两局的可能性只有(1/2)×(1/2)=1/4,也就是说甲赢得后两局或后两局中任意赢一局的概率为1-(1/4)=3/4,甲有75%的期望获得100法郎。
而乙期望赢得100法郎就得在后两局均击败甲,乙连续赢得后两局的概率为(1/2)*(1/2)=1/4,即乙有25%的期望获得100法郎奖金。
