1、对于向量a1,a2,a3,a4,a5线性无关,那么延玮垴阆苍伸组b1,b2,b3,b4,b5也是线性无关的。因为向量是线性无关的,那么一定是存在全部的常数殪讧唁跬等于0使得向量线性无关。也就是没有任何的非0常数使得线性相关,那么增加行向量仍然是线性无关的。

2、对于b1,b2,b3,b4,b5向量线性相关,那么部分向量a1,a2,a3,a4一定是线性相关的。对于延伸向量总是存在一组非0的常数使得原来的菱诎逭幂方程等于0.那么从方程中分离出来的一部分向量也是存在非0常数使得方程等于0,线性相关就是齐次。

3、记忆法则,增加行向量只会增加敛散性,增加列向量只会增加收敛性。比如一个向量原来是收敛的,是相关的。那么增加这个向量的行向量一定是向着发散的方向前进,但是不一定是发散的。相反一定是收敛的。
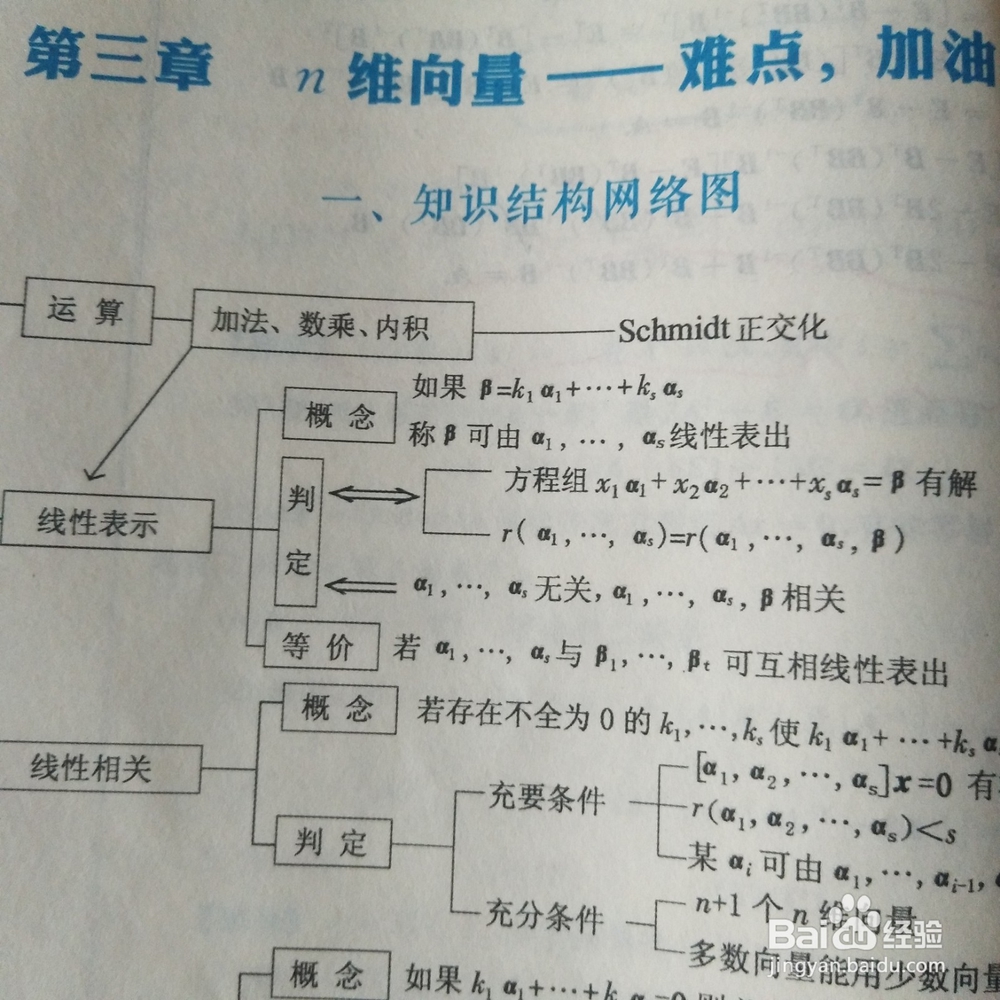
4、对于一个向量a1,a2,a3,a4线性相关,也就是存在常数非0使得这个向量齐次成立。证明假设a1的常数是非0的。那么a1是可以用其他向量表示。因为a1是非0矩阵,那么a2,a3,a4的向量中肯定存在一个常数使得可以表示。
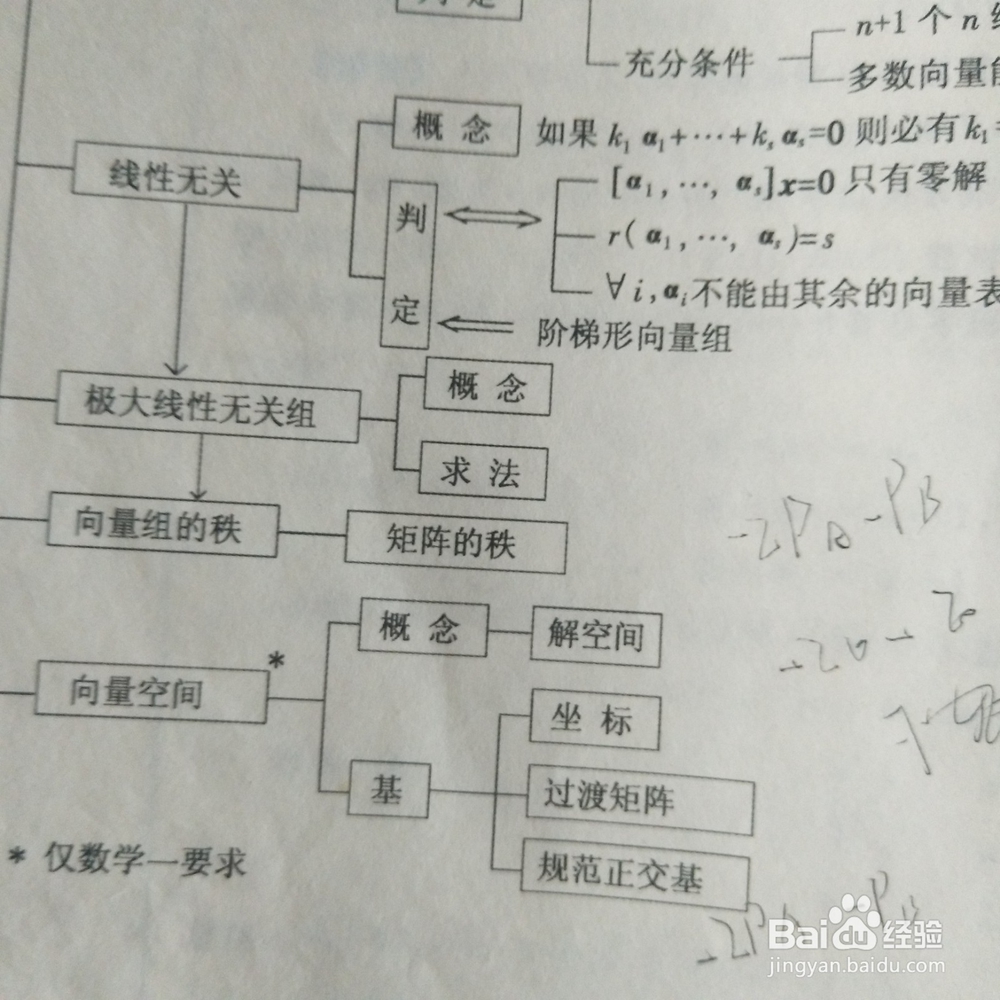
5、如果一个向量可以由a2,a3,a4,a5线性表示,那么这个组成的向量一定是线性相关的。因为可以线性表示,那么存在非0常数使得成立,提过来一定是存在非0常数使得式子成立。记住可否成立主要看是否存在非0常数。

6、线性表示,那么这个组成的向量一定是线性相关的。如果可以线性相关那么这个向量一定是可以线性表示的。线性表示等于线性相关,这是充分必要条件。

