如果一元n次方程(n∈N﹢)的一边只有含未知数的一项和非零的常数项,另一边是零,那么这样的方程就叫做二项方程。
形如axn+b=0的方程,其中n为正整数,a、b≠0。将原方程化为xn=-ba的形式后,用复数开n次方的方法即可求解。它是用代数方法解一元n次方程的基础。
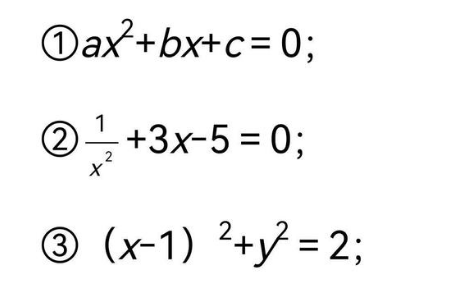
解一元二项方程的方法
一、因式分解法
一元二次方程ax+bx+c=0(a≠0) 化为如(mx-n)(dx-e)=0的形式可 以直接求得解为x=n/m,或x=e/d。
例如:3x-3x=0, 化为3x(x-1)=0。积为0,则有两种可能,3x=0或x-1=0
得出答案:x=0 或x=1
二、直接开平方;
(x-m)=n (n≥0)一元二次方程可以直接开平方法求得解为x=m±√n
例如:(x-1)=4 得出x-1=±2,即x=3或x=-1
