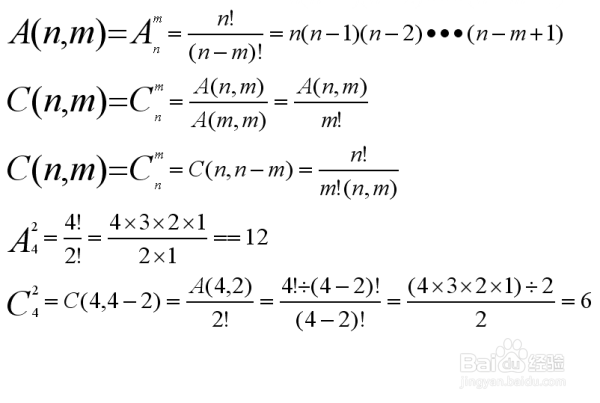看了对排列组合的介绍,只有定义与公式,完全是程序化的说明,发现自己理解的很费力。 为了辅助对排列组合定义的理解,小编用具体的例子来说明它的定义。并列出了详细的计算过程。
排列的定义及其计算公式
1、 排列有两种定义,但计算方法只有一种,凡是符合这两种定义的都用这种方法计算。 定义的前提条件是罪焐芡拂m≦n,m与n均为自然数。① 从n个不同元素中,任取m个元素按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。② 从n个不同元素中,取出m个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数。③ 用具体的例子来理解上面的定义:4种颜色按不同颜色,进行排列,有多少种排列方法,如果是6种颜色呢。从6种颜色中取出4种进行排列呢。 解:A(4,4)=4x(4-1)x(4-2)x(4-3)x(4-4+1)=4x1x2x3x1=24。 A(6,6)=6x5x4x3x2x1=720。 A(6,4)=6!/(6-4)!=(6x5x4x3x2x1)/2=360。

2、[计算公式]排列用符号A(n,m)表示,m≦n。计算公式是:A(n,m)=n(n-1)(n-2)……(n-m+1)=n!/(n-m)!此外规定0!=1,n!表示n(n-1)(n-2)…1例如:6!=6x5x4x3x2x1=720,4!=4x3x2x1=24。

组合的定义及其计算公式
1、 组合的定义有两种。定义的前提条件是m≦n。① 从n个不同元素中,任取m个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合。② 从n个不同元素中,取出m个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数。③ 用例子来理解定义:从4种颜色中,取出2种颜色,能形成多少种组合。解:C(4,2)=A(4,2)/2!={[4x(4-1)x(4-2)x(4-3)x(4-4+1)]/[2x(2-1)x(2-2+1)]}/[2x(2-1)x(2-2+1)]=[(4x3x2x1)/2]/2=6。

2、[计算公式]组合用符号C(n,m)表示,m≦n。公式是:C(n,m)=A(n,m)/m! 或 C(n,m)=C(n,n-m)。例如:C(5,2)=A(5,2)/[2!x(5-2)!]=(1x2x3x4x5)/[2x(1x2x3)]=10。

其它排列与组合公式
1、其它排列与组合有三种。① 从n个元素中取出m个元素的循环排列数=A(n,m)/m!=n!/m!(n-m)!。② n个元素被分成K类,每类的个数分别是n1,n2,…,nk这n个元素的全排列数为n!/(n1!xn2!x…xnk!)。③ k类元素,每类的个数无限,从中取出m个元素的组合数为C(m+k-1,m)。
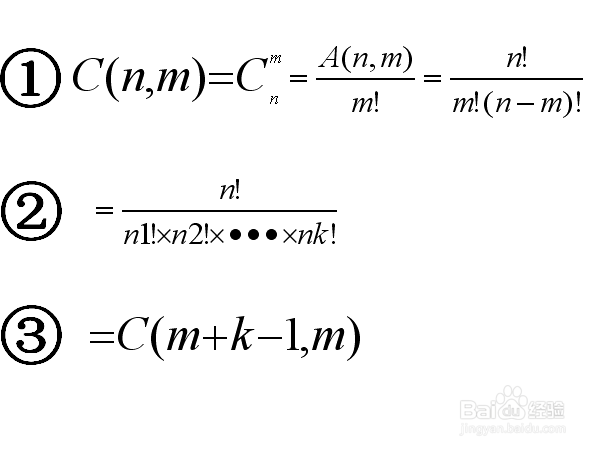
符号说明
1、C-代表-Combination--组合数A-代表-Arrangement--排列数(在旧教材为P-permutation--排列)N-代表-元素的总个数M-代表-参与选择的元素个数!-代表-阶乘
基本公式整理
1、只要记住下面公式,就会计算排列组合:(在列式中n为下标,m为上标)排列A(n,m)=n(n-1)(n-2)……(n-m+1)=n!/(n-m)!组合C(n,m)=A(n,m)/A(m,m)=A(n,m)/m!C(n,m)=C(n,n-m)=n!/m!(n,m)!例如A(4,2)=4!/2!=4x3=12C(4,2)=4!/(2!x2!)=(4x3x2)/(2x2)=6