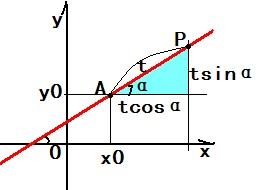
设直线过定点P（x0巳呀屋饔,y0）,则A对应的参数是t1 ,B对应的参数是t2；
且|AP|=|t1|,|BP|=|t2|，假设|t1| >|t2|,
当A，B醐蛑臀谁位于P的同侧时，t1,t2同号，|AB|=|AP|-|BP|=|t1|-|t2|=|t1-t2|；
当A，B位于P的异侧时，t1,t2异号，|AB|=|AP|+|BP|=|t1|+|t2|=|t1-t2|。
扩展资料：
一般地，在平面直角坐标系中，如果曲线上任意一点的坐标x、y都是某个变数t的函数：
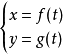
并且对于t的每一个允许的取值，由方程组确定的点(x, y)都在这条曲线上，那么这个方程就叫做曲线的参数方程，联系变数x、y的变数t叫做参变数，简称参数。相对而言，直接给出点坐标间关系的方程叫普通方程。
曲线的极坐标参数方程ρ=f(t),θ=g(t)。
圆的参数方程 x=a+r cosθ y=b+r sinθ（θ∈ [0，2π) ） (a,b) 为圆心坐标，r 为圆半径，θ 为参数，(x,y) 为经过点的坐标。
椭圆的参数方程 x=a cosθ y=b sinθ（θ∈[0，2π）） a为长半轴长 b为短半轴长 θ为参数 。
（椭圆）
双曲线的参数方程 x=a secθ （正割） y=b tanθ a为实半轴长 b为虚半轴长 θ为参数。
抛物线的参数方程 x=2pt^2 y=2pt p表示焦点到准线的距离 t为参数。
直线的参数方程 x=x'+tcosa y=y'+tsina,x',y'和a表示直线经过（x',y'），且倾斜角为a,t为参数。
或者x=x'+ut， y=y'+vt (t∈R)x',y'直线经过定点（x',y'),u，v表示直线的方向向量d=(u,v)。
圆的渐开线x=r(cosφ+φsinφ） y=r(sinφ-φcosφ）（φ∈[0,2π）） r为基圆的半径 φ为参数。
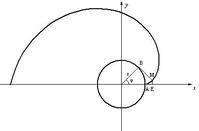（圆的渐开线）
平摆线参数方程 x=r（θ-sinθ） y=r（1-cosθ）r为圆的半径，θ是圆的半径所经过的角度（滚动角），当θ由0变到2π时，动点就画出了摆线的一支，称为一拱。
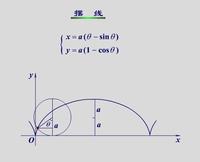（平摆线）
