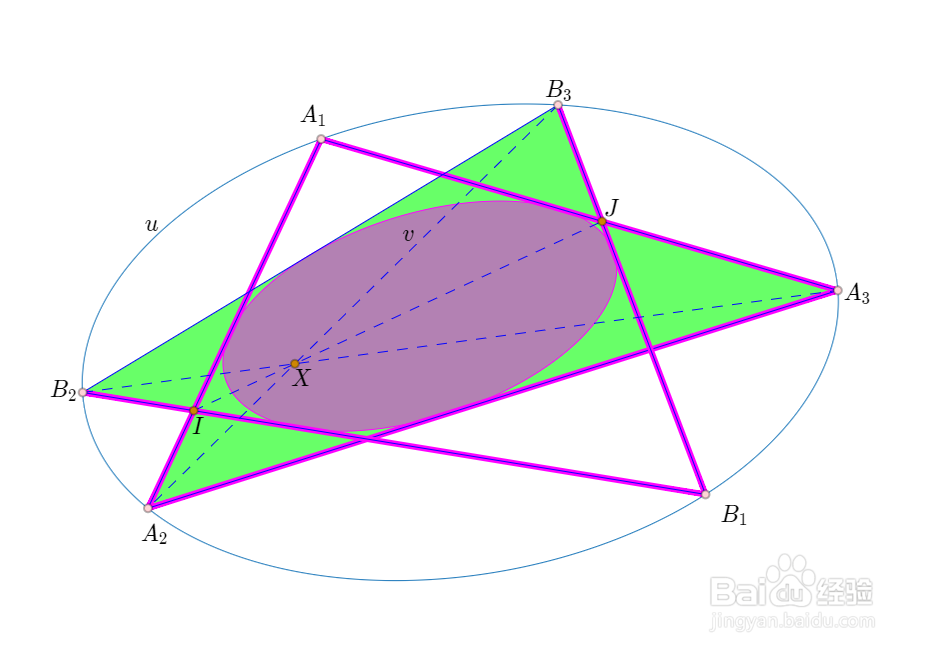
1、先介绍两个引理。Pascal定理:互不重合的六点A1、A2、A3、B1、B2、B3在同一个非退化的圆荨页呷窍锥曲线上,其充要条件是,A1A2与B1B2的交点I、A1A3与B1B3的交点J、B2A3与A2B3的交点X,这三点共线。
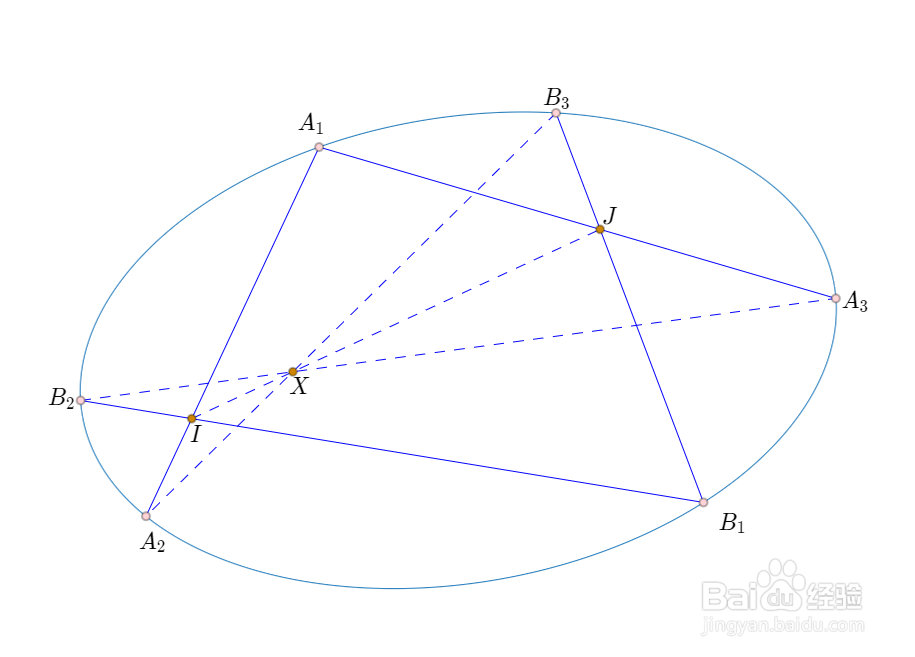
2、Brianchon定理:六边形A2IB2B3JA3的六条边,和同一个非退化的圆锥曲线相切,其充要条件是,三条主对角线B2A3、A2B3、IJ三线共点。仔细看下图,找出这个六边形。
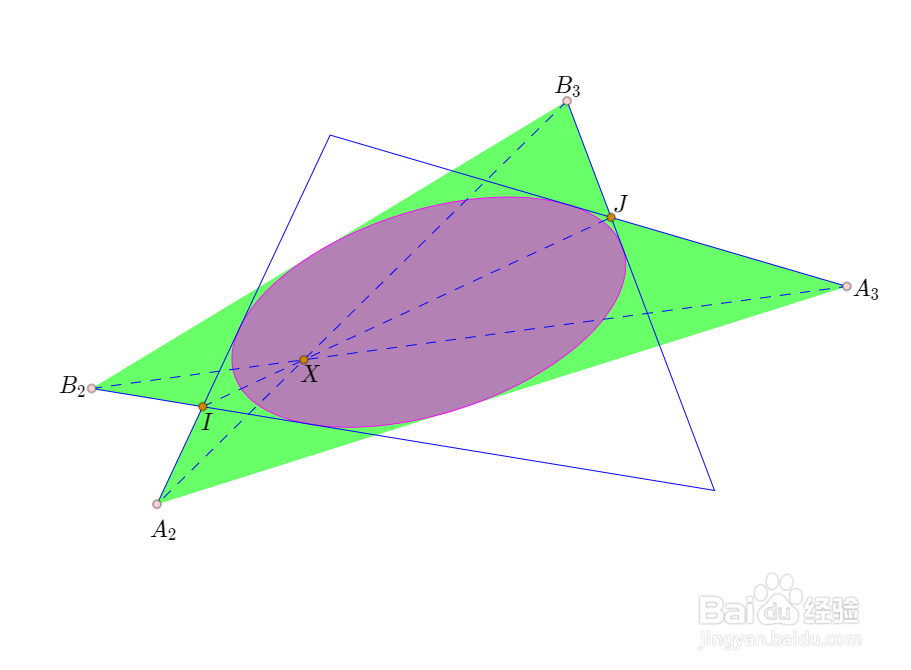
3、三边形的Poncelet闭合定理:互不重合的六点A1、A2、A3、B1、B2、B3都在圆锥曲线u上,且A1A2A3的三边与圆锥曲线v相切。如果B1B2和B1B3都与v相切,那么B2B3也与v相切。
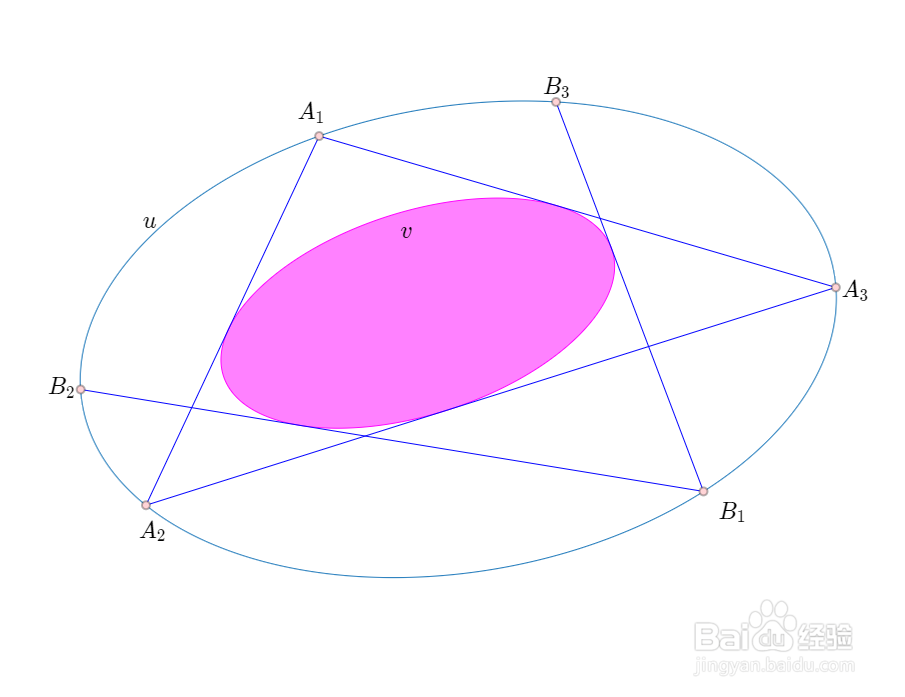
4、下面开始分两步来证明:先连接B2A3和A2B3,交点记为X;设A1A2和B1B2交于I,A1A3和B1B3交于J,那么根据Pascal定理,有:I、J、X共线。
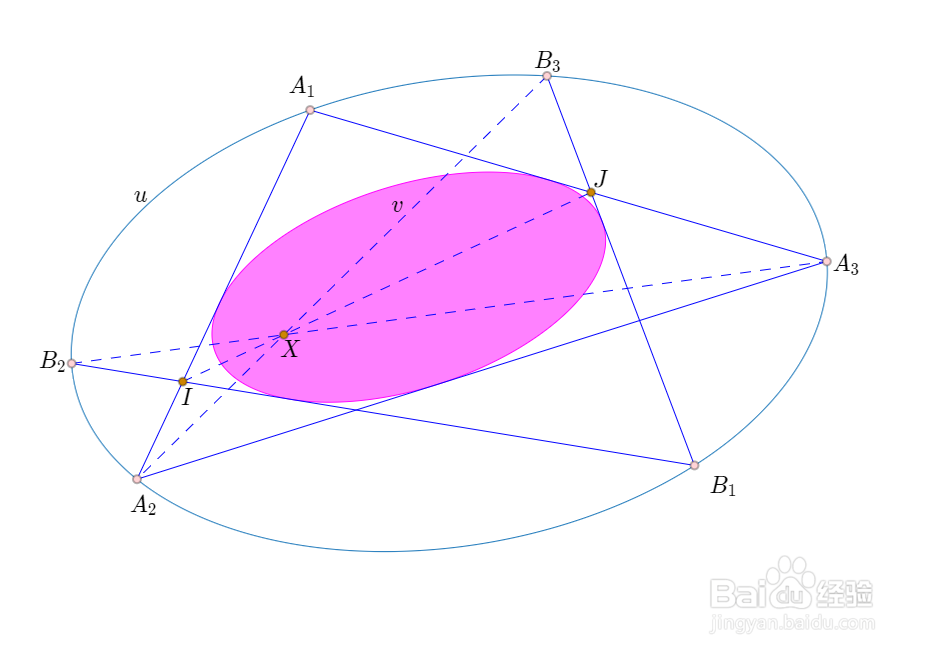
5、考察六边形A2IB2B3JA3,其三条主对角线B2A3、A2B3、IJ三线共点,因此六边相切于同一个圆锥曲线。
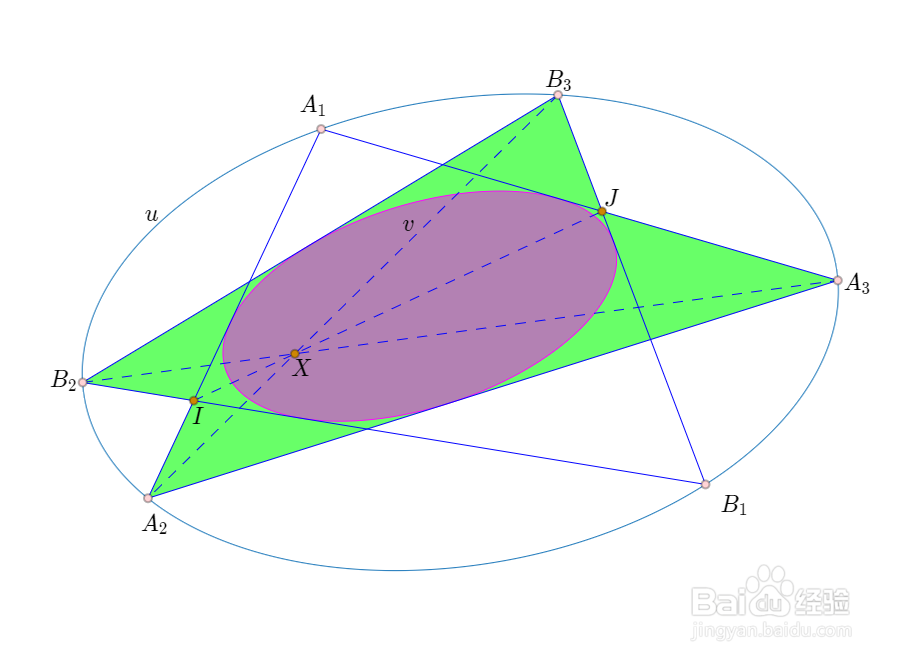
6、因为五条切线A1A2、A2A3、A3A1、B1B2、B1B3确定了唯一的圆锥曲线v,因此B2B3也与v相切。