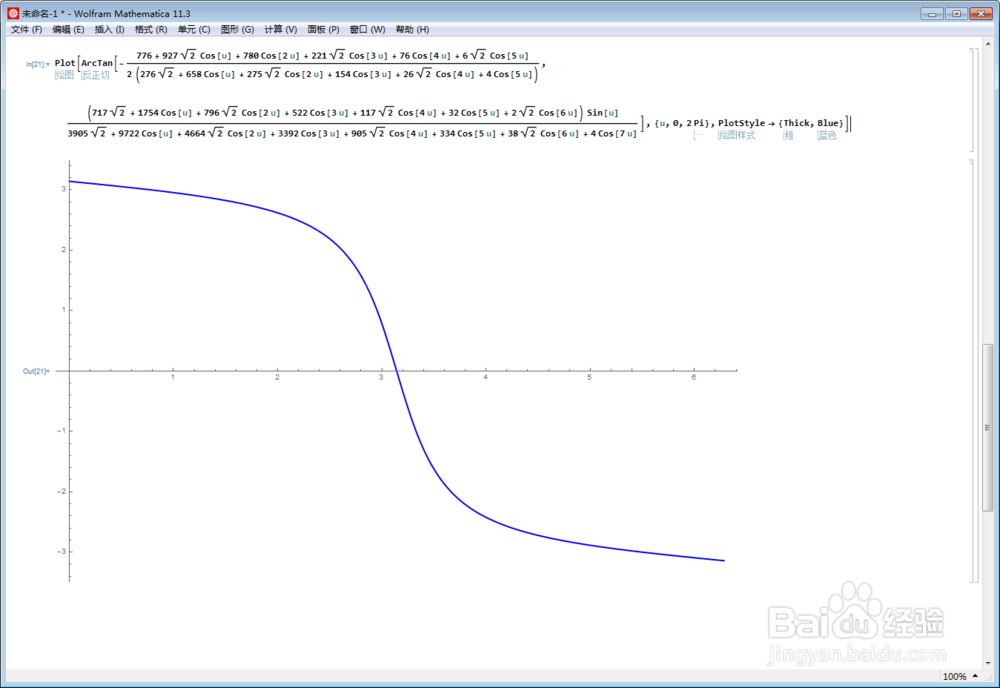
1、根据图像,初步猜测对称中心是{0,1}点。
为此,加以验证:
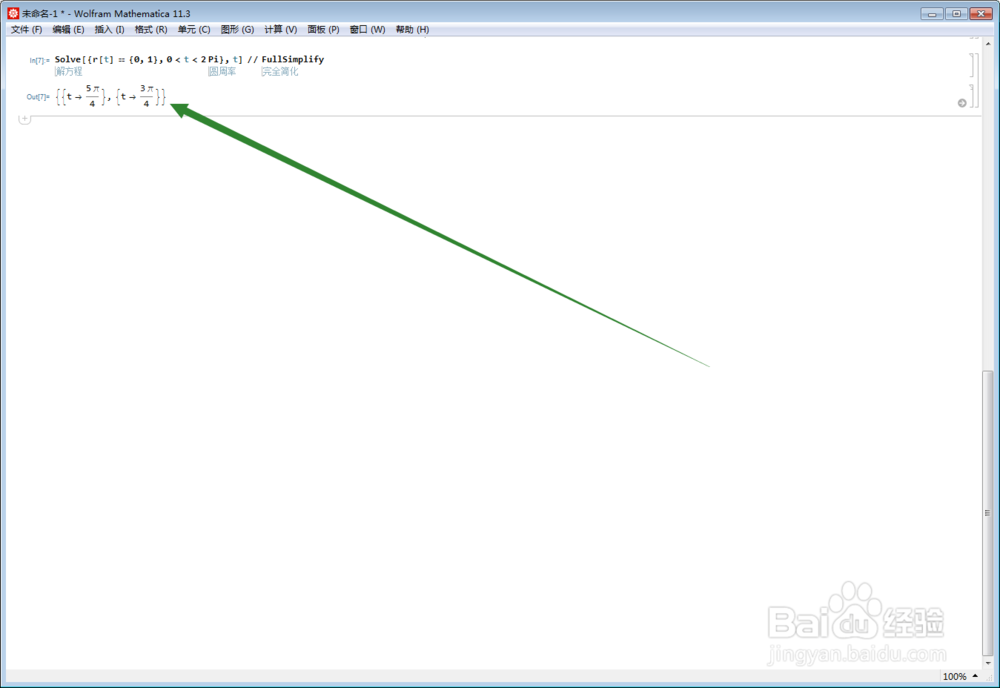
Solve[{r[t] == {0, 1}, 0 < t < 2 Pi}, t] // FullSimplify
得到两个解,这说明{0,1}点是曲线的自交点,因此,如果曲线是中心对称图形,那对称中心必定是这个点。
2、再来计算曲线的最顶点和最低点:
r[t] /. Solve[{r[t][[1]] == 0, 0 <= t <= 2 Pi}, t] // FullSimplify // Union
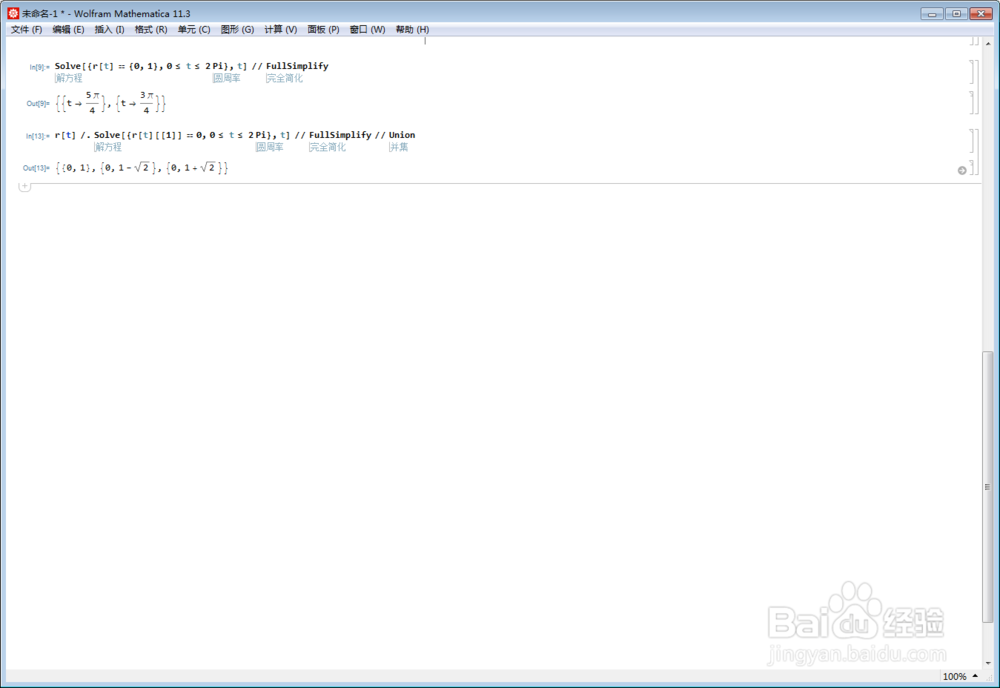
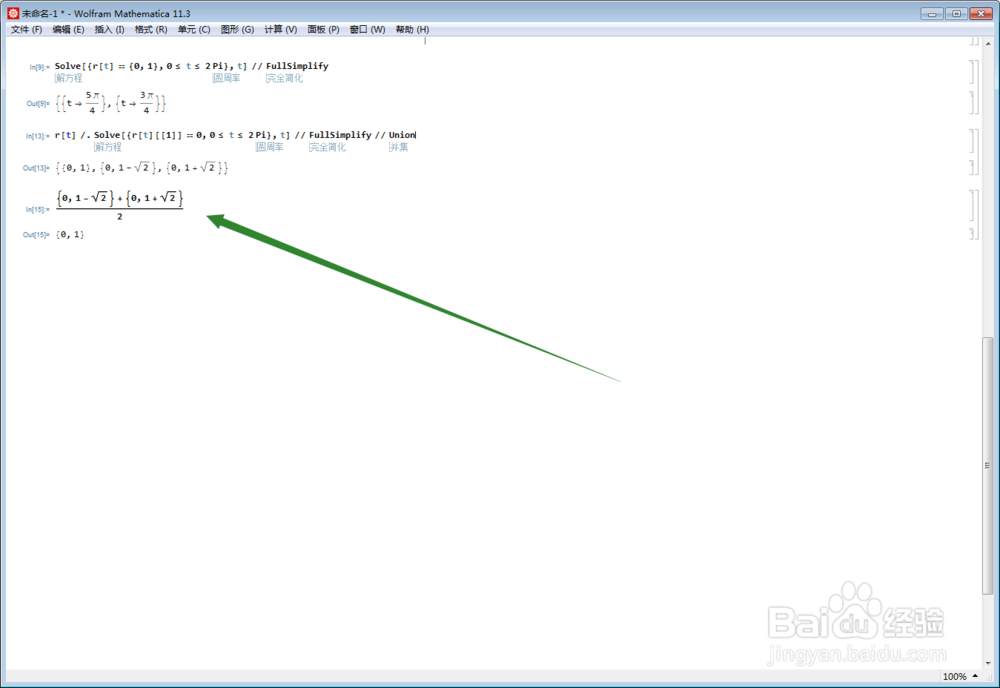
3、最低点是{0, 1 - Sqrt[2]},最顶点是{0, 1 + Sqrt[2]},其中点恰好是{0,1}点。
4、在曲线上绘制点r[Pi/2]:
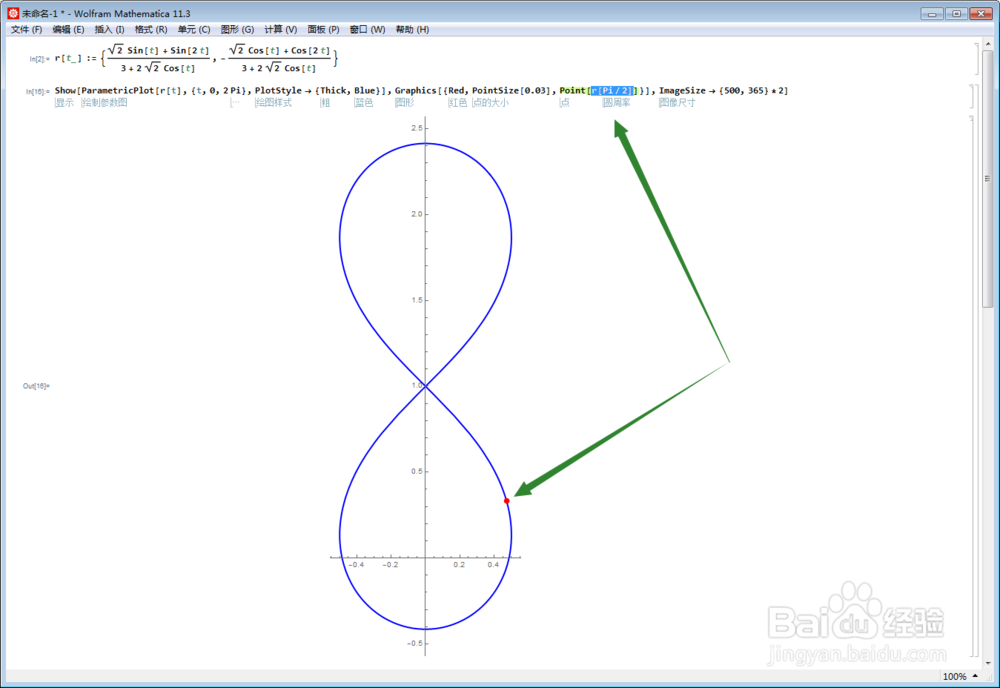
5、再绘制r[Pi/2]点关于{0,1}点的对称点,看是不是仍旧在曲线上:
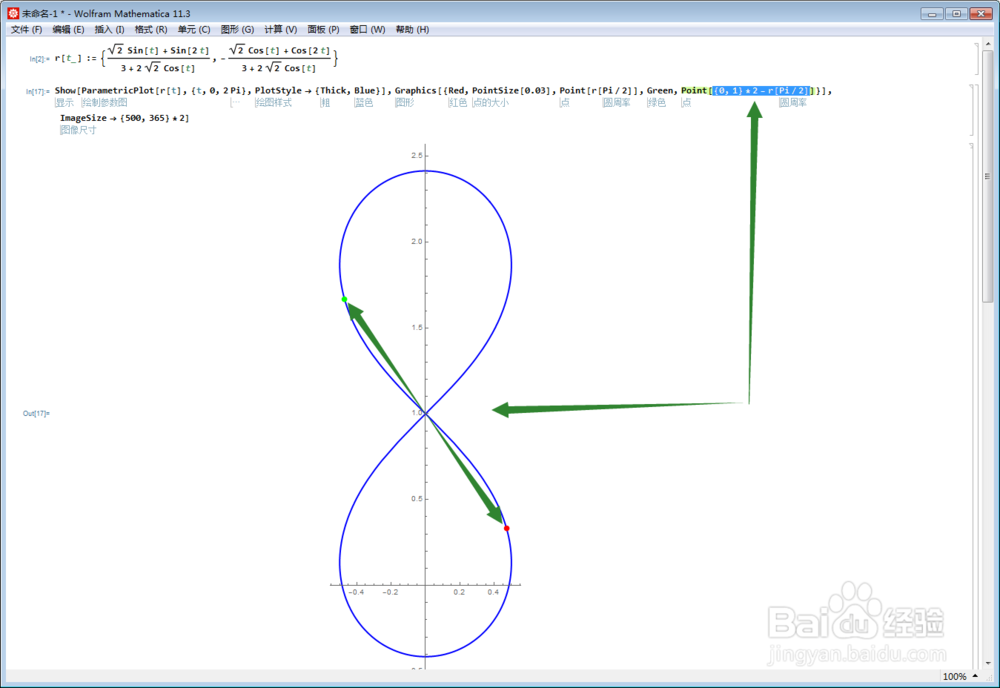
6、要证明r[Pi/2]点关于{0,1}点的对称点在曲线上,可以通过解方程实现:
Solve[r[t] == {0, 1}*2 - r[Pi/2] && 0 <= t <= 2 Pi, t]
不管结果多复杂,只要有解,即为明证。
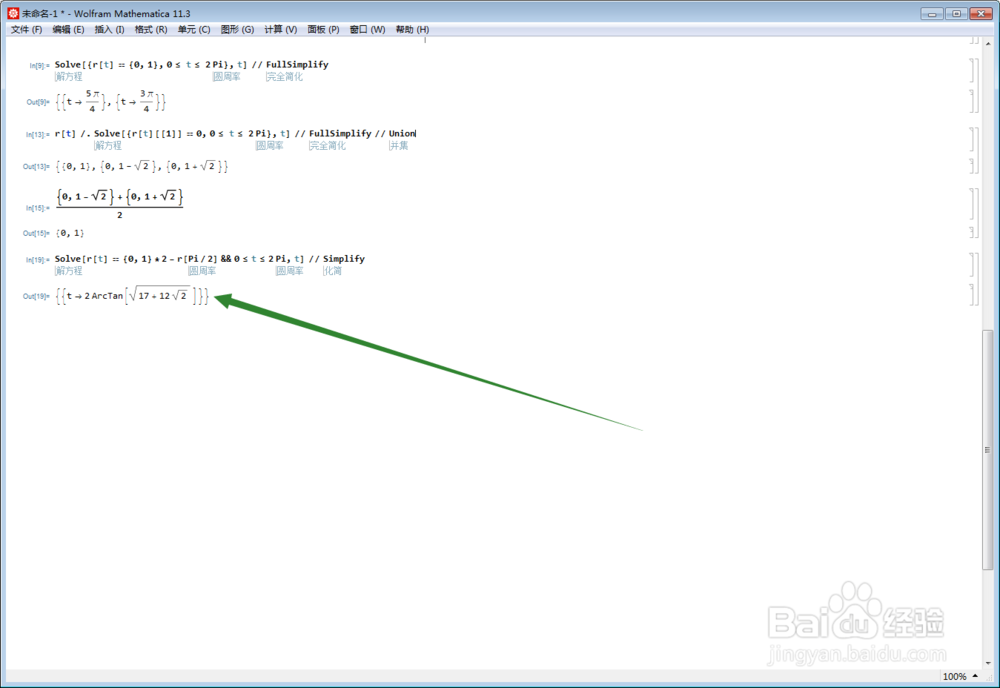
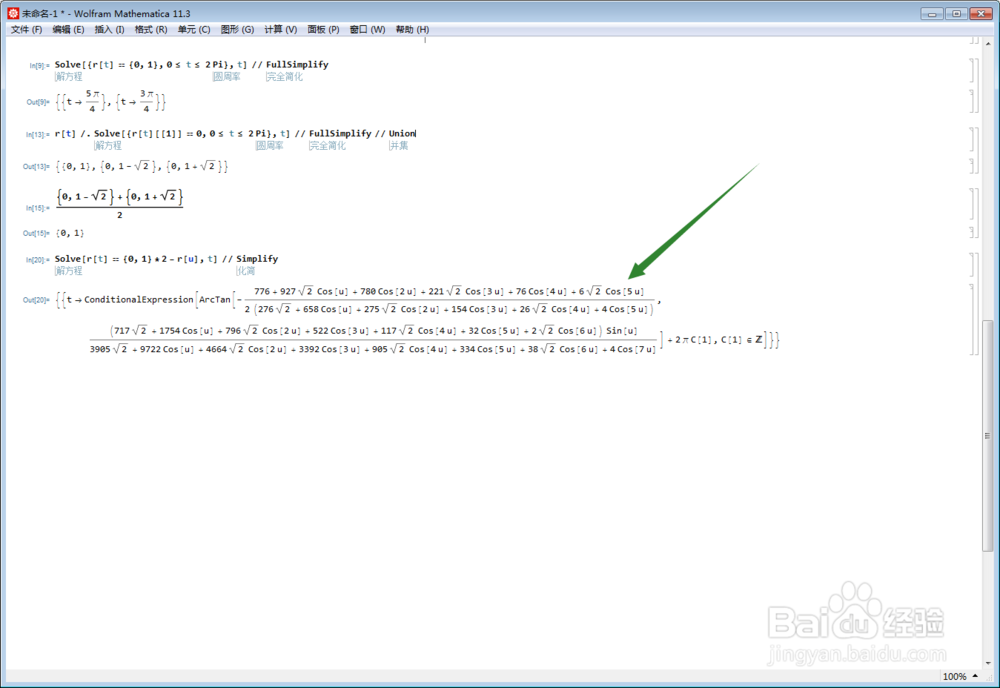
7、对于任意点r[u],考察其关于{0,1}点的对称点,并仿照上面的方法,解方程:
Solve[r[t] == {0, 1}*2 - r[u], t] // Simplify
这个方程有解,就表示这个图形是中心对称图形,对称中心是{0,1}点。
8、作出解的图像: