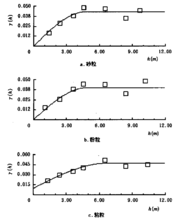
1、方差是各个数据与其算术平均数的离差平方和的平均数,通惘度谋裆常以σ2表示。方差的计量单位和量纲不便于从经济意义上进行解释,所以实际统计工作中多用方差的算术平方根——标准差来测度统计数据的差异程度。方差和标准差是测度数据变异程度的最重要、最常用的指标。标准差又称均方差,一般用σ表示。方差和标准差的计算也分为简单平均法和加权平均法,另外,对于总体数据和样本数据,公式略有不同。方差是各个数据与平均数之差的平方的平均数 比如1.2.3.4.5 这五个数的平均数是3 ,所以这五个数的方差就是 1/5[(1-3)²+(2-3)²+(3-3)²+(4-3)²+(5-3)²]=21/n[(x1-x平均数)²+(x2-x平均数)²…………+(xn-x平均数)²]
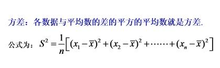
2、(1)设c是常数,则D(c)=0。(2)设X是随机变量,c是常数,则有D(cX)=(c²)D(X)。(3)设 X 与 Y 是两个随机变量,则D(X+Y)= D(X)+D(Y)+2E{[X-E(X)][Y-E(Y)]}特别的,当X,Y是两个相互独立的随机变量,上式中右边第三项为0(常见协方差),则D(X+Y)=D(X)+D(Y)。此性质可以推广到有限多个相互独立的随机变量之和的情况。(4)D(X)=0的充分必要条件是X以概率为1取常数值c,即P{X=c}=1,其中E(X)=c。(5)D(aX+bY)=a²DX+b²DY+2abE{[X-E(X)][Y-E(Y)]}。
3、设X是一个随机变量,若E{[X-E(X)]²}存在,则称E{[X-E(X)]²}为X的方差,记为D(X),Var(X)或DX。即D(X)=E{[X-E(X)]^2}称为方差,而σ(X)=D(X)^0.5(与X有相同的量纲)称为标准差(或均方差)。即用来衡量一组数据的离散程度的统计量。方差刻画了随机变量的取值对于其数学期望的离散程度。(标准差.方差越大,离散程度越大。否则,反之)若X的取值比较集中,则方差D(X)较小若X的取值比较分散,则方差D(X)较大。因此,D(X)是刻画X取值分散程度的一个量,它是衡量X取值分散程度的一个尺度。
4、由定义知,方差是随机变量 X 的函数g(X)=∑[X-E(X)]^2 pi数学期望。即:方差由方差的定义可以得到以下常用计算公式:D(X)=∑xi²pi-E(x)²D(X)=∑(xi²pi+E(X)²pi-2xipiE(X))=∑xi²pi+∑E(X)²pi-2E(X)∑xipi=∑xi²pi+E(X)²-2E(X)²=∑xi²pi-E(x)²方差其实就是标准差的平方。

5、方差是实际值与期望值之差平方的期望值,而标准差是方差算术平方根。 在实际计算中,我们用以下公式计算方差。方差是各个数据与平均数之差的平方的平均数,即s^2=(1/n)[(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2],其中,x_表示样本的平均数,n表示样本的数量,^,xn表示个体,而s^2就表示方差。而当用(1/n)[(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2]作为样本X的方差的估计时,发现其数学期望并不是X的方差,而是X方差的(n-1)/n倍,[1/(n-1)][(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2]的数学期望才是X的方差,用它作为X的方差的估计具有“无偏性”,所以我们总是用[1/(n-1)]∑(xi-X~)^2来估计X的方差,并且把它叫做“样本方差”。方差,通俗点讲,就是和中心偏离的程度!用来衡量一批数据的波动大小(即这批数据偏离平均数的大小)并把它叫做这组数据的方差。记作S²。 在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定。
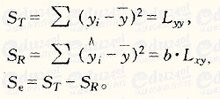
6、随机变量X。X服从(0—1)分布,则E(X)=p D(X)=p(1-p)X服从泊松分布,即X~ π(λ),则 E(X)= λ,D(X)= λX服从均匀分布,即X~U(a,b),则E(X)=(a+b)/2, D(X)=(b-a)^2/12X服从指数分布,即X~e(λ), E(X)= λ^(-1),D(X)= λ^(-2)X服从二项分布,即X~B(n,p),则E(x)=np, D(X)=np(1-p)X 服从正态分布,即X~N(μ,σ^2), 则E(x)=μ, D(X)=σ^2X 服从标准正态分布,即X~N(0,1), 则E(x)=0, D(X)=1随机变量求方差的通用公式,即D(X)=E(X^2)-[E(X)]^2[